
This is why the function notation is useful: it makes it clear which symbols are bound as parameters and which are free.
#Quadratic function formula free
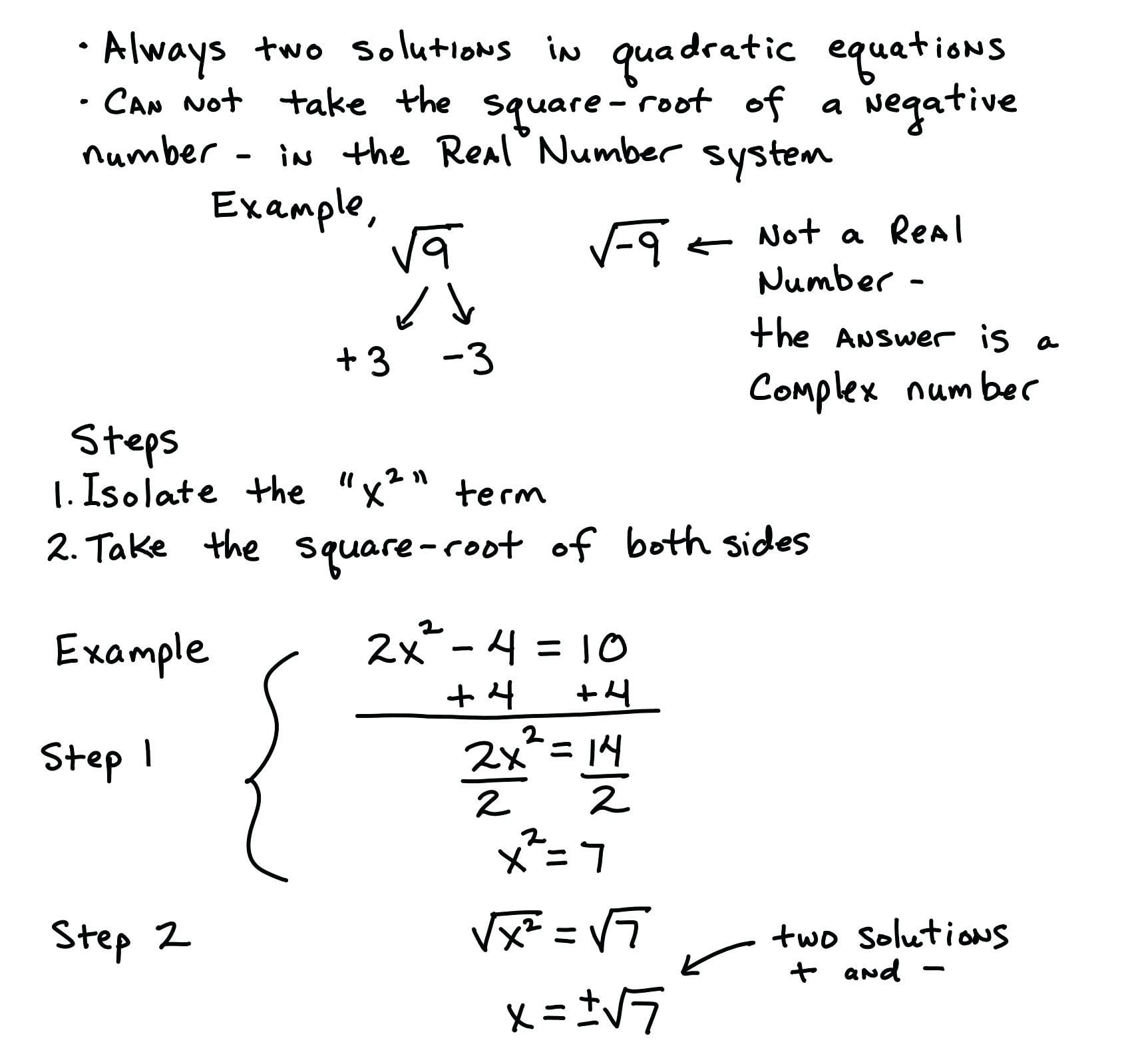
It could easily be a function of three variables $f(a, b, c) = ax^2 + bx + c$, where $x$ is a constant, or a free variable which parametrizes the function. Usually something which looks like $ax^2 + bx + c$ is a function of $x$, and the $a, b, c$ are coefficients, but that is not necessarily so we are prejudiced toward interpreting it that way because it resembles a common convention. Some of the symbols might be considered to be held constant. If we are confronted with a formula with multiple symbols, like $ax^2 + bx + c$ then it is not clear how it is intended to be used as a function. There is one variable in it, so if it is going to be a function, that variable is it. For instance, the quadratic formula $x^2 + 2x + 1$ will serve us as a function of $x$. The equation has a close relative, the inequality, which is a statement that one quantity is greater than or less than another.Īn expression, or formula, however can be a function, if we make it clear which variables in that formula are to serve as parameters.

Specifically, it is a statement which asserts that two mathematical expressions denote objects or quantities which are equal: equation is the situation of of making two equal.
An equation is a logical statement, and as such it is either true or false.

Equations are usually not functions (see below).


 0 kommentar(er)
0 kommentar(er)
